Continuidad de una funcion

 INIDE.

Clase 2.

Jorge Armando Orbe Hernández.

Calculo Diferencial.

Continuidad de una función.

Podemos decir que una función es continua cuando en su grafica no aparecen saltos, no existen huecos ( la grafica se puede dibujar sin levantar el lápiz de la hoja de papel.

 Se dice que una función f(x) es continua si o solo si cumple con estas 3 condiciones

1) La función f(x) esta definida en el punto a es decir para el punto x=a existe la imagen f(x).

                                             F(a)

2) El limite L de la función f(x) cuando x tiende al punto a existe, por tanto sus limites laterales son iguales, es decir:

3)El limite L de f(x), cuando x tiende al punto a sea igual al valor f(x)

Para algunas familias de funciones es posible conocer su continuidad basándose en  los siguientes criterios generales:

1.Las funciones polinómicas son continuas en todo el conjunto de los números reales.

2.Las funciones racionales obtenidas como cociente de dos polinomios son continuas en el conjunto R. a excepción de aquellos en los que se anula el denominador.

3.Las funciones potenciales, exponenciales y logarítmicas son continuas en todo su dominio de definición. 

4. Las funciones trigonométricas seno y coseno son continuas en todo el conjunto de los números reales( a excepción de la tangente que discontinua en los valores múltiplos impares de π/2)  

Propiedades de las funciones continuas.

Dadas las funciones f(x) y g(x) continuas en un punto o intervalo que cumple entonces que:

1) La suma o resta de ambos es una función continua en es punto o intervalo.

2) El producto de las dos funciones es una función continua en ese punto o intervalo.

3)El cociente entre ambas funciones es una función continua en ese punto o intervalo excepto en aquellas en las que el denominador se anula.

4)Si f(x) es continua en a y g(x) es continua en f(a) entonces la composición de funciones (g ° f)(x) es también continua en a.

Discontinuidad

Toda función que en un punto dado no cumpla con  algunas de las condiciones de la continuidad  es decir que  presenta un punto en el que existe un salto y la grafica se rompe se le denomina función discontinua.

Discontinuidad evitable

Toda función que en un punto dado no cumple alguna de las condiciones necesarias para la continuidad se denomina discontinua. Cuando la discontinuidad se debe al hecho de que existe el límite de la función en el punto, pero la función no está definida para el mismo, se habla de discontinuidad evitable.

Para obtener una nueva función que sea continua también en el punto de discontinuidad evitable, se procede del modo siguiente:

1)      Se calcula el valor del límite de la función en el punto a.

             Se añade el punto a al dominio de definición de la función, y se le asigna el valor:

      

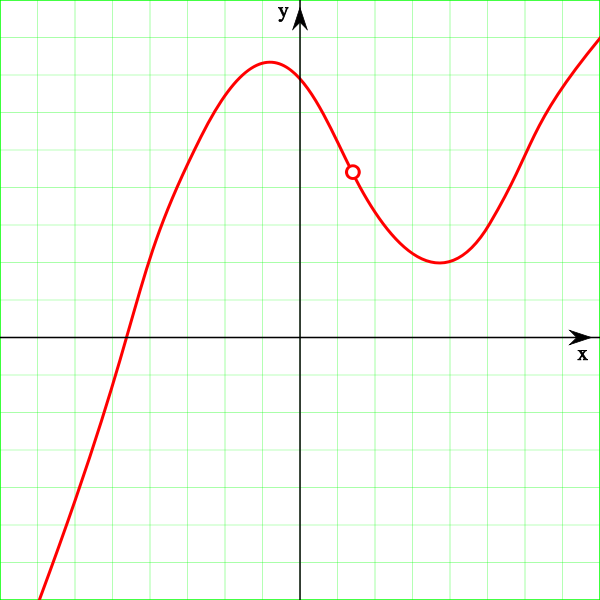
La función f (x) presenta una discontinuidad evitable en el punto x = 2. F(x) sería continua en R.

Discontinuidades no evitables

Existen otros tipos de discontinuidades que no pueden resolverse, por lo que se llaman discontinuidades no evitables. Estas discontinuidades se clasifican en:

1)Discontinuidades de salto: cuando existen ambos límites laterales (por la derecha y por la izquierda), pero no coinciden.

2)Discontinuidades asintóticas: cuando el límite es infinito.

3)Discontinuidades por el dominio de definición: cuando existe el límite y la función está definida en el punto, pero ambos valores no coinciden.

En sentido genérico, se llama discontinuidad de segunda especie a la que tiene lugar cuando uno de los límites laterales es finito y el otro es infinito o no existe

 

Referencias

Continuidad de funciones - hiru

Continuidad de Funciones (uson.mx)

Continuidad de funciones | Superprof

Continuidad de una funcion.pdf (matematicasonline.es)

Bibliografía

df. (111). fdfdf. grg: grtt.

Samuel Fyelabrada de la Vega Truciós. (2008). Calculo Diferencial tercera edicion. Mexico DF: McGRAW-HILL Interamericana Editores S,A de C.V.